Wie kommt das Bild ins Mathe-Arbeitsblatt
Mathebilder sind immer eine Herausforderung. Lange Internetsuchen oder Handarbeit sind weitverbreitet. Manchmal ist das auch die schnellste Möglichkeit.
Aber man hätte es ja doch gern digital, abspeicherbar, änderbar. Und oft gibt es dafür eine einfache Möglichkeit.
1. PowerPoint statt Word
PowerPoint lässt sich über den Reiter Entwurf > Foliengröße auf A4 und auf Hochformat umstellen. Im Gegensatz zu Word bietet es
- viel mehr grafische Bausteine,
- frei auf dem Blatt platzierbare Textblöcke/Aufgaben
- die beliebte eingekringelte Aufgabennummerierung findet sich unter Einfügen > Symbole > Symbol > eingekreiste alphanumerische Zeichen.
- Brüche und Formeln lassen sich ebenfalls als eigene Blöcke einfügen und optimal platzieren.
- Kästchenpapier-Blöcke können als Tabelle erzeugt und beliebig platziert werden.
Die beliebte Tägliche Übung im A5-Format lässt sich über eine A4-Querformat-Folie realisieren. Diese lässt sich schön auf der Tafel anzeigen. Auf 2 Folien verdoppelt, in Acrobat konvertiert und dann 2 in 1 ausgedruckt entstehen aus derselben Folie dazu passende A5 Arbeitsblätter.
Wahrscheinlichkeitsbäume und Zahlenstrahle lassen sich relativ gut über die Funktion ‚Start > Anordnen > ‚horizontal verteilen‘ erzeugen. Für die Ticks des Zahlenstrahls kopiere einen Tick einfach so oft, wie Ticks gebraucht werden, schiebe sie dann grob an ihren Platz und richte sie mit ‚oben ausrichten‘ und ‚horizontal verteilen‘ genau aus.
Soll das Bild (Rechteck, Kreis usw.) exakte Maße haben, geht dies über die rechte Maustaste mit Form formatieren. Dann lassen sich die Maße genau eingeben. Erfolgt die Konvertierung in pdf über ’speichern unter‘ bleiben die exakten Maße erhalten. Bei der Export-Funktion ist dies nach meiner Erfahrung nicht immer der Fall.
2. Geogebra
Besonders Konstruktionen und Funktionsgraphen lassen sich sehr einfach mit Geogebra erstellen und von dort entweder über das Sniping-Tool oder über den Bildexport in PowerPoint integrieren.
Mit Geogebra lassen sich auch schöne „Virtual-Reality“-Effekte erzeugen, z.B. die Elipse auf dem Schrägbild des Frühstückstellers oder die Parabel im Wasserfall.
Schwieriger wird es, wenn das Bild vorgegebene Längen haben soll, die der Schüler möglicherweise auch messen soll. Dazu muss das Geogebra-Bild auf die genauen Maße skaliert werden.
Nach Einfügen des Bildes in PowerPoint kannst du eine Linie auf das eingefügte Geogebrabild legen. Sie muss die zu kontrollierende Bildlinie deckungsgleich überlagern:
Die Länge der Powerpoint-Linie zeigt PowerPoint an. Die Strecke von A nach B ist hier absolut etwa 10 cm lang (Satz des Pythagoras). Soll diese Länge im Ausdruck 6 cm betragen, muss du die Breite des Bildes mit dem Faktor 6 / 10 skalieren. Die Breite des Bildes wird unter Bildformat angezeigt. Gib einfach die neue Sollbreite ein. Die PowerPoint-Hilfslinie kannst du dann wieder löschen.
Genauso können auch aus dem Internet genommene Bilder auf die gewünschten Absolutlängen skaliert werden.
3. Fertige Bildersammlungen
Eine vollständige Bruchsammlung nach Nennern geordnet von 0/1, 1/1, 0/2, 1/2, 2/2 ….11/12, 12/12 findest du auf dieser Seite unter Downloads. Weiterhin kannst du natürlich auch alle interaktiven Tafelbilder dieser Seite nach Bedarf einstellen und dann mit der rechten Maustaste herunterladen (Lizenz: CC BY-NC).
4. Latex mit LibreOffice
Manche mögen Latex. Damit kann jede noch so komplizierte Formel perfekt gesetzt werden und es gibt eine eigene Bibliothek namens Tikz zum Erzeugen von Bildern.
Du musst deshalb nicht das ganze Arbeitsblatt mit LateX erzeugen. Bei wenigen Formeln und Bildern geht es auch so:
- Arbeitsblatt zunächst im Wesentlichen (bis auf Formeln und nicht PowerPoint-konforme Bilder) in PowerPoint erstellen.
- LibreOffice – Impress hat ein LaTeX-Addin, damit kannst du fehlende Formeln und Bilder mit LaTeX als eingebettete svg-Bilder erzeugen.
- Diese kannst du dann in PowerPoint mit Strg + C -> Strg + V hineinkopieren.
Installiere dafür zunächst MikTeX und LibreOffice von ihren jeweiligen Homepages. Du benötigst dann die LibreOffice-Erweiterung TeXMath.
Öffne nach der Installation ein LibreOffice Dokument (z.B. Impress) und klicke auf das Formelsymbol. Es öffnet sich ein Fenster ‚TeXMathGleichung‘. Dort gibst du gleich deinen Latex-Code ein. Zunächst klicke jedoch auf Präamble und prüfe, ob die nötigen usepackages vorhanden sind. Für Bilder benötigst du tikz; amsmath ist für die Doppelstrichbuchstaben für reelle Zahlen, ganze Zahlen usw. verantwortlich. Je nach Komplexität der Bilder brauchst du mehr Bibliotheken.
Bei mir sieht es so aus:
\usepackage{amsmath}
\usepackage{amssymb}
\usepackage{array}
\usepackage[usenames]{color}
\usepackage{ifxetex}
\usepackage{siunitx}
\usepackage{tikz}
\usepackage{pgfplots}
\usetikzlibrary{math, calc,intersections, quotes, angles, shapes.misc}
\usepackage{tikz-3dplot}
% XeLaTeX compiler
\ifxetex
\usepackage{fontspec}
\usepackage{unicode-math}
% Uncomment these lines for alternative fonts
%\setmainfont{FreeSerif}
%\setmathfont{FreeSerif}
% LaTeX compiler
\else
% Uncomment this line for sans-serif maths font
\everymath{\mathsf{\xdef\mysf{\mathgroup\the\mathgroup\relax}}\mysf}
\fi
\definecolor{hellblau}{HTML}{7aefff}In das Fenster TeXMath-Gleichung gibst du den LateX-Code ein. Setze auf der rechten Seite das Häkchen für Transparenz, dann hat deine Grafik einen transparenten Hintergrund und verdeckt nicht unnötig Text.
Hier z.B. der Code für ein paar konzentrische Kreise (Dartscheibe):
\begin{tikzpicture}[x=1cm, y=1cm, line width=2mm]
\path [draw=black,fill=yellow] (0,0) circle (3cm);
\path [draw=black,fill=red] (0,0) circle (2cm);
\path [draw=black,fill=green, line width=3mm] (0,0) circle (1cm);
\draw [thin,gray] (-4,-4) grid (4,4);
\end{tikzpicture}Oder eine Figur, die durch Verbinden von Punkten im Koordinatensystem entsteht:
\begin{tikzpicture}[x=1cm, y=1cm]
\draw [draw=black, fill=lightgray]
(0,0) -- (3,0) -- (3,3) -- (2,3) -- (2,2) -- (0,2) -- cycle;
\end{tikzpicture}Oder einfach eine coole Formel:
\int_2^{\infty}{\frac{x^3}{x^5 -7} dx}Das Ergebnis ist jeweils ein skalierbares, eingebettetes svg-Bild. Dieses lässt sich in jedes Officedokument mit Strg + C und Strg + V kopieren:
Eine TikZ-Einführung mit vielen Beispielbildern auf der Basis von LibreOffice findest du hier unter Downloads.
Wenn du ein Dokument mit vielen Formeln und Bildern erstellen willst, ist es möglicherweise sinnvoller, dieses ganz in LibreOffice zu erstellen. Sollen die absoluten Längen aller Figuren stimmen, musst du entweder direkt mit LateX arbeiten oder die Bilder nachträglich richtig skalieren. Wenn die Bilder keinen Rand haben, geht das sehr einfach über rechte Maustaste > Größe und Position.
5. 3-dimensionale Bilder mit Latex
Bei dem in der Schule verwendeten Schrägbild wird die x- und y-Richtung unverzerrt abgebildet, die z-Richtung wird im 45° Winkel und auf die Hälfte verkürzt angetragen.
Wenn du in Latex eine Figur im 3-dimensionalen Raum beschreibst, d.h. 3-dimensionale Koordinaten verbindest, wird die resultierende Figur automatisch mit einer Axiometrie auf den 2-dimensionalen Raum projiziert. Allerdings stimmen die Parameter der Projektion nicht mit dem in der Schule geforderten Schrägbild überein. Damit dies der Fall ist, muss die Richtung und Skalierung der x-, y- und z-Achse explizit vorgegeben werden. Dies erfolgt durch die Parameter von tikzpicture:
\begin{tikzpicture}[
x={(1cm,0cm)},%x-Achse unverzerrt in x-Richtung
y={(0cm,1cm)}, %y-Achse unverzerrt in y-Richtung
z={({0.5*cos(45)},{0.5*sin(45)})}, %z-Achse im 45°-Winkel auf die Hälfte verkürzt
scale = 0.8% Skalierung des Bildes
]Die Koordinaten werden dann 3-dim deklariert: \coordinate[label={above right}:{$A$}] (A) at (1.5,3,4);
Das Schrägbild von runden Körpern wie Kugel und Zylinder sieht nicht gut aus, siehe dazu den Beitrag 3-dim Anschauung und das Schrägbild. Deshalb ist es hier üblich, eine Orthogonalprojektion zu zeigen. Die 3-dim Darstellungen von Geogebra sind immer Orthogonalprojektionen.
Bei einer Orthogonalprojektion wird der Körper zunächst so gedreht, dass ein guter räumlicher Eindruck entsteht, dann werden die x- und y-Koordinaten abgetragen, wie sie sich nach der Drehung ergeben, die z-Koordinate entfällt.
Das tikz-3dplot-Paket erlaubt es, den Körper 3-dimensional zu beschreiben (dabei legt man ihn so, dass dies möglichst einfach möglich ist) und dann die Drehung des Körpers vorzugeben. Das Paket ermittelt dann automatisch die sich ergebende Orthogonalprojektion.
- Synthax: \tdplotsetmaincoords{θd}{φd}
- θd Winkel (in Grad) um den das Koordinatensystem um die x-Achse gedreht ist.
- φd Winkel (in Grad) um den das Koordinatensystem um die z-Achse gedreht ist.
6. Videos, Verlinkungen, QR-Codes und andere Gimmicks
Bildschirmaufnahme
Mit PowerPoint kann man sehr einfach eine Bildschirmaufnahme machen. Gehe einfach auf den Reiter Einfügen > Aufzeichnen und dann auf Bildschirmaufnahme. Mit Windows + Shift + Q beendest du die Aufnahme. Sie wird automatisch in die PowerPoint eingefügt und kann mit rechter Maustaste > Medien speichern unter als .mp4-Datei gespeichert und überall wieder eingefügt werden. Zahlreiche Internetplattformen ermöglichen die kostenlose Konvertierung in eine .gif-Datei.
Links und QR-Codes
Zahlreiche andere Internetseiten ermöglichen es, kostenlos aus einer beliebigen Internetadresse einen QR-Code zu erzeugen, der dann als Bild eingefügt werden kann. Für alle Übungen auf dieser Seite klicke dafür einfach im Menü rechts auf QR-Code anzeigen.
Einem eingefügten Bild oder Piktogramm kann mit der rechten Maustaste ein Link hinzugefügt werden, so dass der Nutzer mit Klick auf das Bild auf diese Ressource gelenkt wird. Der Link kann zu einem Dokument im Laufwerk, zu einer Internet-Ressource oder auch zu einer anderen Seite desselben Dokuments führen. Natürlich kann ein Link auch einfach mit einem Linktext eingefügt werden. Das geht über Einfügen > Link.
Eingabefelder
In eine PowerPoint-Datei können keine Eingabefelder eingefügt werden, die bei einer Konvertierung in .pdf erhalten bleiben. Öffne dafür die PowerPoint-Datei in LibreOffice. Die Konvertierung klappt mittlerweile sehr gut. Selten musst du etwas am Format nachoptimieren. In Libreoffice kannst du über den Reiter Extras Eingabefelder, Auswahlfelder, Ankreuzkästchen und dergleichen hinzufügen. Bei der Konvertierung in .pdf bleibt alles erhalten und du erhältst ein schönes interaktives Arbeitsblatt.
7. Wie habe ich das Titelbild erzeugt?
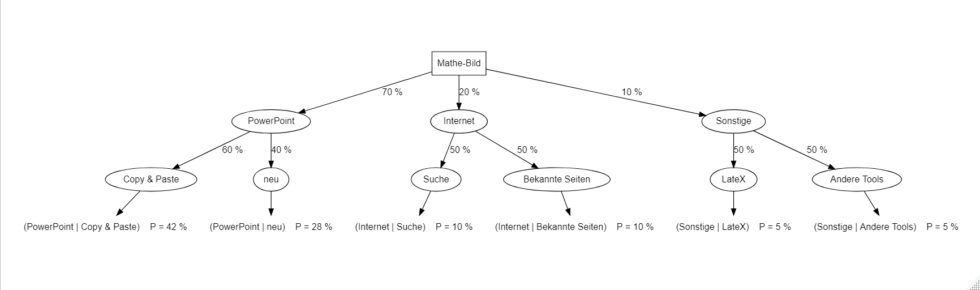
Den Wahrscheinlichkeitsbaum habe ich mit R-Projekt erzeugt. Code und Anleitung dafür findet sich hier.
8. Du hast einen weiteren Tipp?
Schreibe ihn in den Kommentar..
Dieser Beitrag hat 0 Kommentare