3-dim Anschauung und das Schrägbild

In der Schule beschränkt sich die Darstellung 3-dimensionaler Objekte in der Regel auf das sogenannte Schrägbild. Dabei handelt es sich um eine spezielle Axiometrie, die Fachleuten unter dem Namen Kavalierprojektion bekannt ist.

Die Kavalierprojektion ist einfach durchzuführen und liefert oft einen guten räumlichen Eindruck der abgebildeten Körper. Nichtsdestoweniger weicht sie von dem tatsächlichen bildlichen Eindruck 3-dimensionaler Objekte, wie wir ihn mit dem Auge oder auf einem Foto sehen, stark ab.

Das Schrägbild

Beim in der Schule gelehrten Schrägbild werden Längen in zwei Richtungen (links und oben) unverzerrt abgebildet. Die Tiefe wird im 45° Winkel nach hinten und auf die Hälfte verkürzt abgetragen.

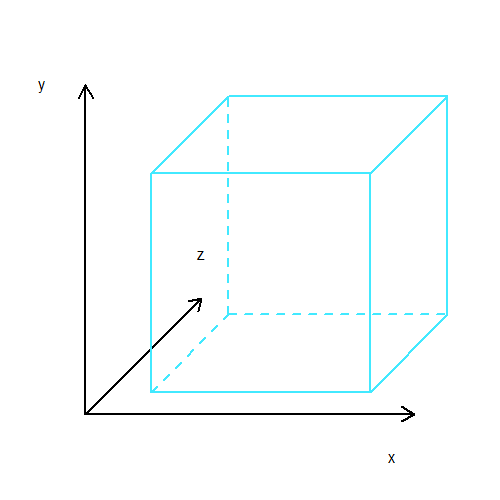
Diese Art der Darstellung von 3-dimensionalen Objekten hat auch außerhalb der Schulmathematik große Verbreitung. Sie ist zum Beispiel Gegenstand einer DIN-Norm (Deutsche Industrienorm: ISO 5456-3). So werden technische Zeichnungen angefertigt.

Der Vorteil dieser Darstellung ist, dass sie einen guten räumlichen Eindruck des Körpers gibt, aber die Vorderseite unverzerrt darstellt. Wir kennen derartige Darstellung aus Aufbauanleitungen von Ikea und anderen technischen Anleitungen. Die unverzerrte Vorderseite erleichtert es, zu erkennen, wo Details wie Schrauben oder Löcher genau positioniert sind / werden sollen, der räumliche Eindruck, der durch die verkürzt dargestellte Tiefe erzeugt wird, erleichtert das Erkennen des richtigen Objekts und die Groborientierung darauf.

Die Kavalierprojektion hat jedoch auch Nachteile. So werden Kreise und Rundungen nicht gut wiedergegeben, wenn sie sich nicht gerade in einer unverzerrt wiedergegebenen Ebene befinden. Hier eine Kugel zunächst in der üblichen Darstellung als Orthogonalprojektion (auch Parallelprojektion) und dann als Kavalierprojektion:

In der Kavalierprojektion ist der Umriss der Kugel nicht ganz rund, sondern vielmehr eine Elipse: breiter als hoch.

Noch weniger gut macht sich die Kavalierprojektion bei einem Zylinder, hier wieder zunächst in Orthogonalprojektion, dann als Kavalierprojektion:

Konturlinien

Die Abbildungen des Zylinders weisen auf ein Thema hin, das in der Schule nicht diskutiert wird: Projiziert man eine Körper mit runden Flächen auf eine Ebene, so wird die Projektion durch Konturlinien begrenzt, die keinen Kanten des Körpers entsprechen.

Bei den vorgehenden Abbildungen des Zylinders wird hier eine Schwierigkeit sichtbar. Bei der Orthogonalprojektion links ist die Projektion offensichtlich durch zwei Seitenlinien begrenzt. Verbunden werden erstens die beiden linken Endpunkte der beiden horizonalen Elipsenachsen und zweitens die beiden rechten Endpunkte dieser Elipsenachsen.

Bei dem Schrägbild rechts ist der Sachverhalt unklar. Nach Logik der Konstruktion werden die beiden schwarz eingezeichneten Seitenlinien gezeichnet. Dies ist richtig, wie man sieht, wenn man den Zylinder in einen Quader einbeschrieben zeichnet. Für sich betrachtet erscheinen jedoch eher die Begrenzungslinien der blau hinterlegten Fläche die korrekten Konturlinien des Zylinders zu sein.

Noch offensichtlicher werden diese Schwierigkeiten bei Darstellungen des Kegels.

Darstellungen des Kegels

Hier eine Darstellung als Orthogonalprojektion und als Schrägbild einmal mit einem Beispiel, wo die Höhe im Verhältnis zum Radius groß ist:

Wie beim Zylinder fallen beim Schrägbild des Kegels die verbeulte Grundfläche und die nicht plausibel erscheinenden Konturlinien auf. Diese Probleme werden noch augenscheinlicher, wenn die Höhe im Verhältnis zum Radius klein wird:

3d-Skizzen

Deshalb wird in der Schule auch für Zylinder, Kegel und Kugel eine andere 3-dim Darstellung gelernt. Die nach hinten weisende y-Achse wird bei diesen runden Formen nicht im 45° Winkel, sondern in vertikaler Richtung nach oben auf die Hälfte verkürzt angetragen. Dies liefert für sich genommen einen schönen 3-dimensionalen Eindruck (sofern man die Konturlinien des Kegels korrekt tangential einzeichnet). Hier Zylinder und Kegel mit jeweils Radius 2 cm und Höhe 4 cm:

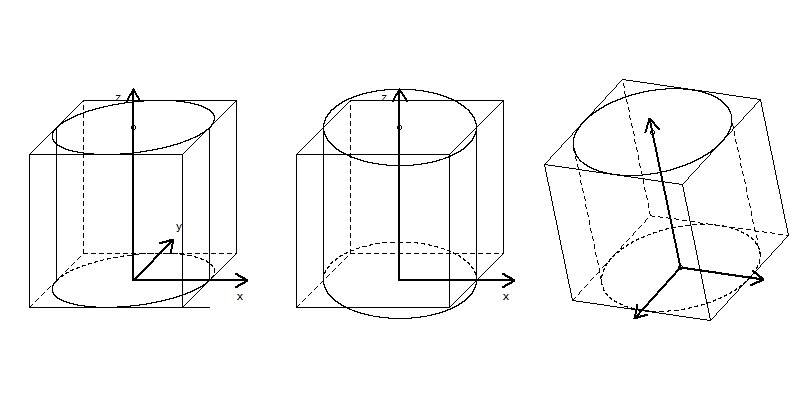
Der Systembruch wird jedoch offenbar, wenn runde Formen und Quader mit ihren nach unterschiedlicher Systematik erzeugten Schrägbildern in einem Bild gezeichnet werden. Im folgenden 3 Bilder eines Würfels mit eingebettetem Zylinder:

• links eine Kavalierprojektion mit der sichtbar unvorteilhaften Wiedergabe des Zylinders
• in der Mitte die ineinandergezeichneten Schrägbilder bzw. Skizzen, wie sie in der Schule gelehrt werden
• rechts eine Orthogonalprojektion. Mit ihr werden beide Körper sehr gut wiedergegeben.

Orthogonalprojektionen

Orthogonalprojektionen entsprechen sehr viel mehr dem, wie wir Körper tatsächlich sehen, als das Schrägbild. Somit sind die Abbildungen im Schulbuch, wenn es sich nicht um Zeichen-Vorlagen handelt, in der Regel Orthogonalprojektionen. Auch Geogebra zeigt uns dynamische Orthogonalprojektionen 3-dimensionaler Körper.

Orthogonalprojektionen sind schon für einfache Körper wie den Würfel nicht einfach von Hand zu zeichnen. Daher wird der Schüler angehalten, Kavalierprojektionen oder Skizzen zu zeichnen, Eines sollte jedoch auch bei einer Skizze beachtet werden:

Ein Kreis ist eine glatte (differenzierbare) Kurve. Die Orthogonalprojektion eines Kreises ist eine Elipse (d.h. sie hat niemals Ecken).

Schnittpunkte von Konturlinien

Während die Projektion von glatten 2-dim Kurven also wieder eine glatte Kurve ergibt, kann der Umriss von einem glatten Körper in der Projektion durchaus Ecken haben. So erscheint das Innere eines Torus in der Projektion in der Regel mit 2 Ecken:

Den Mantel des Torus kann man sich als Umhüllung einer Kugel vorstellen, die auf dem Kreis, in der Mitte des Torus entlangläuft. Dann sieht man dass die umhüllende Kurve der Torusprojektion eine Parallelkurve zu der Projektion des Mittelkreises ist (im Bild rot). Man hat somit für die umhüllenden Kurven der Torusprojektion 3 Fälle:

Das Innere des Torus kann also in der Projektion einen glatten Rand haben, in der Regel hat der Rand der Projektion aber Ecken. Betrachtet man auch die Schatten im Bild oben, versteht man, weshalb der Smiley, den die Mathematiker gewöhnlich in die Torusskizze zeichnen, so gut aussieht:

Der hier genutzte Latex-Code für die Torusdarstellungen findet sich hier:

https://tex.stackexchange.com/questions/348/how-to-draw-a-torus