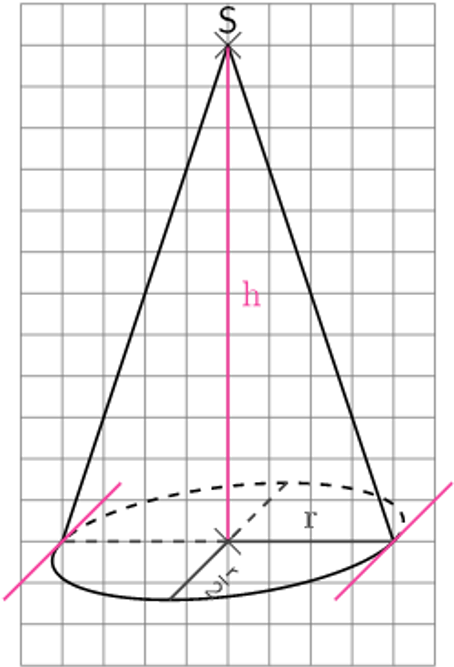
Verschiedene Darstellungen des Kegels
Hier findest du eine Anleitung, wie du verschiedene Darstellungen des Kegels zeichnest.
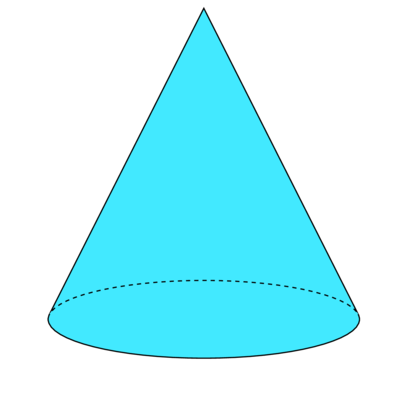
Der Kegel: Draufsicht
Wenn du einen stehenden Kegel genau von oben ansiehst, siehst du eine Kreisscheibe. Das nennt man die Draufsicht.
Achte darauf, den Kreis in der richtigen Größe zu zeichnen: Für einen Kegel mit Höhe h = 6 cm und Radius r = 2 cm, zeichnest du eine Kreisscheibe mit Radius r = 2 cm:
gegeben:
r = 2 cm
h = 6 cm
Draufsicht Kegel:

Der stehende Kegel: Seitenansicht
Wenn du einen stehenden Kegel genau von der Seite ansiehst, siehst du ein gleichseitiges Dreieck. Das nennt man die Seitenansicht.
Achte darauf, das Dreieck in der richtigen Größe zu zeichnen: Für einen Kegel mit Höhe h = 6 cm und Radius r = 2 cm, zeichnest du ein gleichseitiges Dreieck mit Grundseite d = 4 cm und der Höhe h = 6 cm:
gegeben:
r = 2 cm
h = 6 cm
Seitenansicht Kegel:


Der stehende Kegel: Zweitafelbild
Beim Zweitafelbild zeichnest du als erstes die Rissachse. Unten zeichnest du mit einem Abstand von 0,5 cm den Grundriss des Kegels. Dieser entspricht der Draufsicht. Oben zeichnest du mit 0,5 cm Abstand zur Risslinie den Aufriss. Dieser entspricht der Seitenansicht des Kegels.
Achte darauf, beide Figuren mit gleichem Abstand zur Rissachse und genau übereinander zu zeichnen: Die Verlängerung der senkrechten Seiten des Rechtecks bildet eine Tangente an den Kreis.
gegeben:
r = 2 cm
h = 6 cm
Zweitafelbild Kegel:

Das Netz des Kegels
Das Netz des Kegels erhältst du, wenn du den Kegel aufschneidest und glatt streichst.
Das Netz besteht aus der Mantelfläche und der Grundfläche.
Die Mantelfläche ist ein Kreissegment. Der Umfang der Grundfläche passt genau an den Kreisrand der Mantelfläche. Der Radius der Mantelfläche, also des Kreissegments, entspricht der Länge der Mantellinie s des Kegels.
Berechne für die Zeichnung zunächst mit dem Satz des Pythagoras die Länge der Mantellinie s. Wir benötigen weiterhin auch den Winkel des Kreissegments, das die Mantelfläche bildet.
gegeben:
r = 2 cm
h = 6 cm
berechnet:
s =
phi =
Netz Kegel:
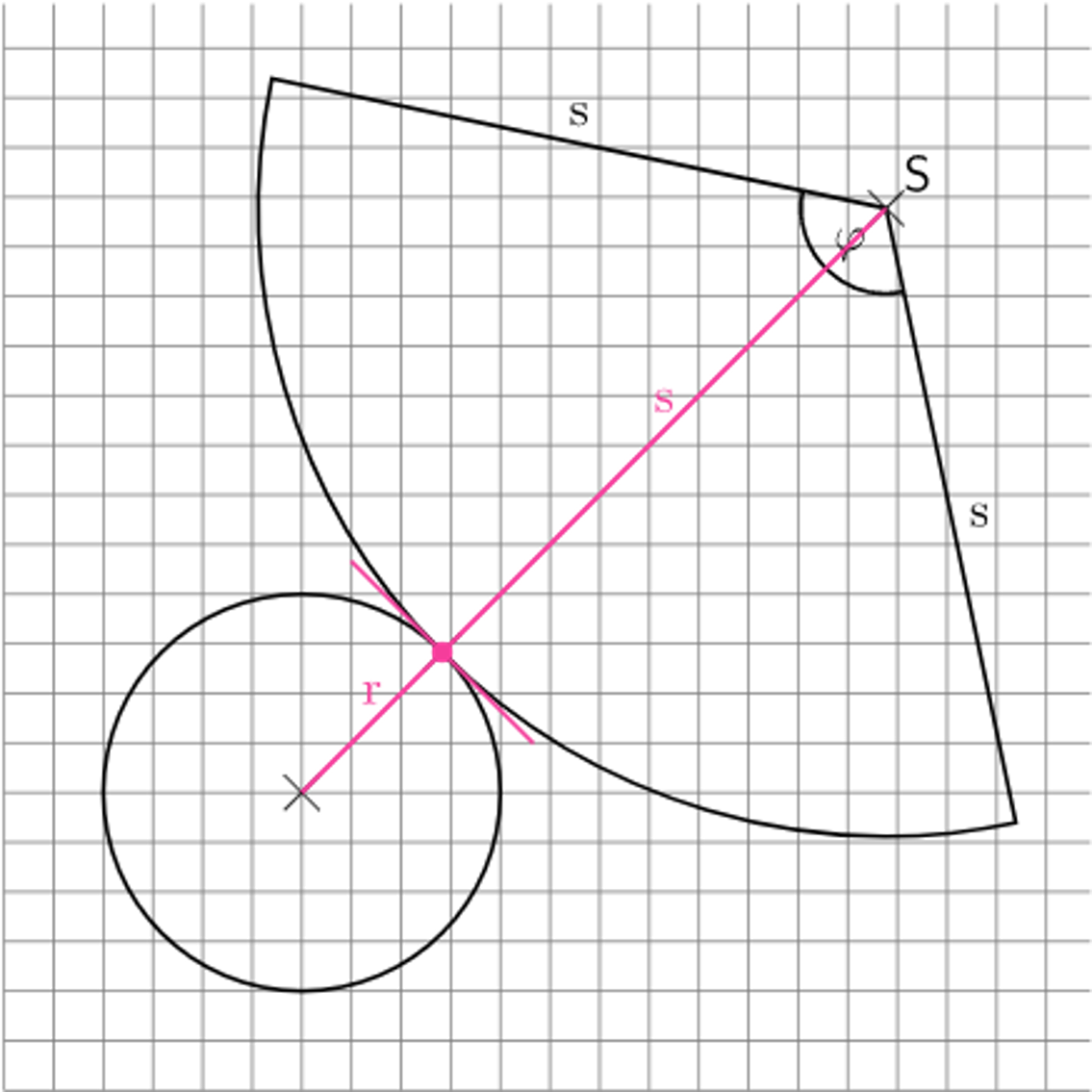
Beginne bei dem Netz mit der Grundfläche, einem Kreis mit Radius r. Zeichne diesen z.B. in die untere linke Ecke deines Blattes.
Zeichne nach oben rechts einen Radius in den Kreis ein und verlängere ihn über den Kreis hinaus um s. Dort liegt die Spitze S.
Zeichne um S einen Kreisbogen mit Radius s.
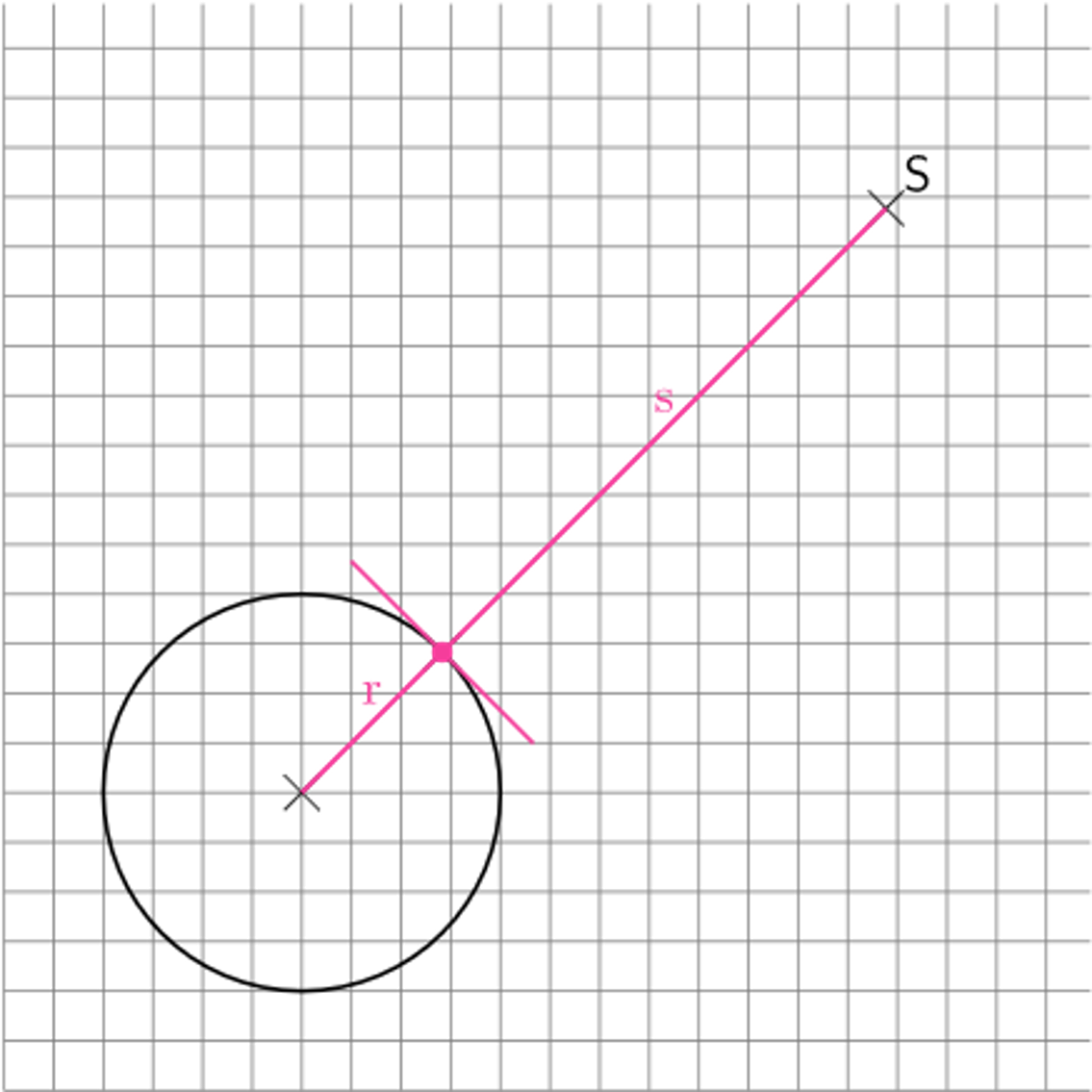
Zeichne in den Kreisbogen um S mit Radius s einen beliebigen Radius ein.
Miss von dort aus den Winkel ab und verbinde.
Du erhältst das Netz:
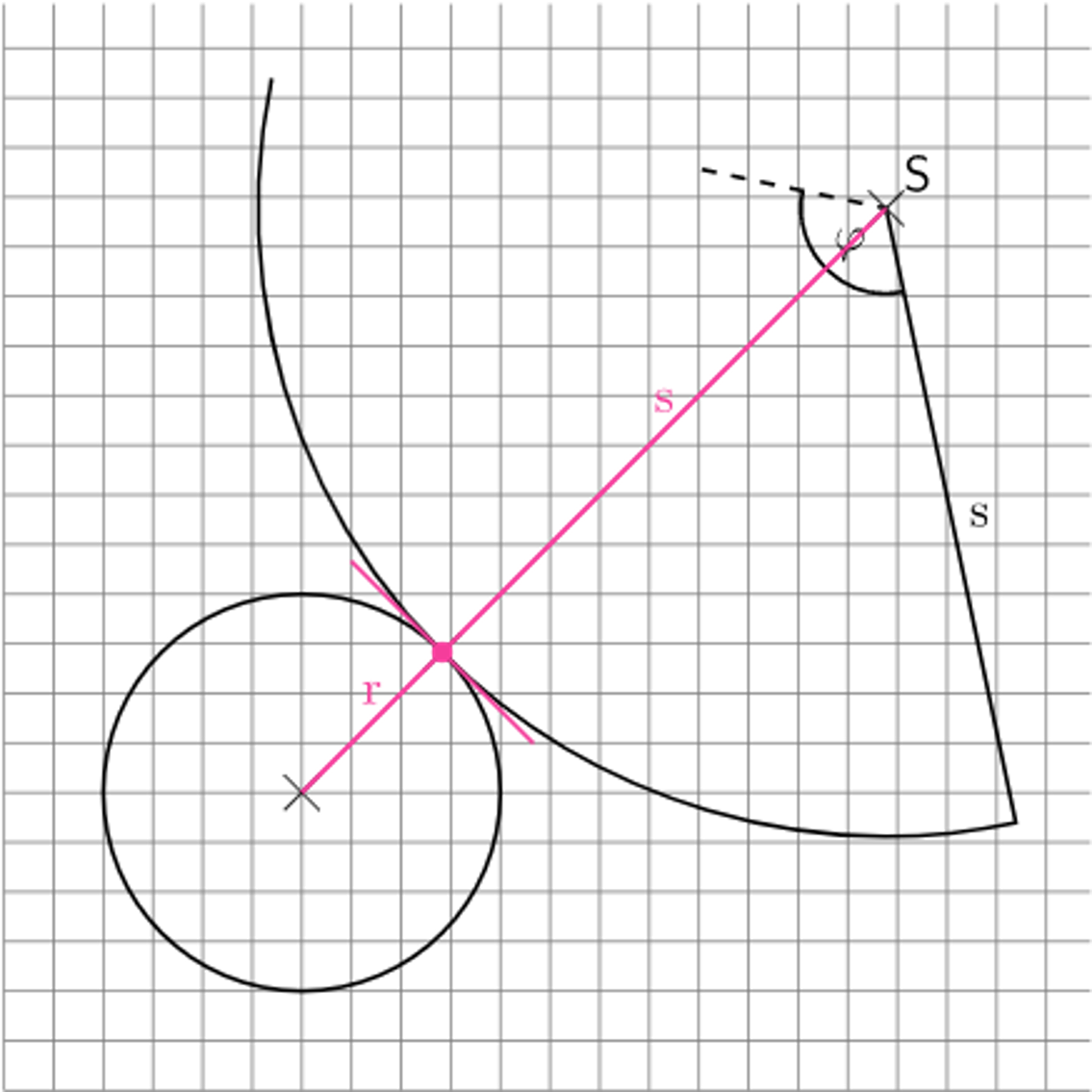
Anmerkungen zum Netz:
Die Länge des Kreisbogens um die Spitze S mit Radius s muss gleich dem Umfang der Grundfläche, einem Kreis mit Radius r sein.
Ein Kreis mit Radius s hat den Umfang .
Der Umfang der Grundfläche ist .
Damit das Kreissegment mit Radius s genau an die Grundfläche passt, muss das Kreissegment ein -tel des vollen Kreises mit Radius sein. Denn .
Der Winkel des Kreissegments ist somit .
3d-Skizze des Kegels
Bei der Skizze des Kreiskegels beginnst du mit der Grundfläche.
Die Grundfläche ist eine Elipse (ein Oval). Die horizontale Durchmesser ist 2r. Der vertikale Durchmesser ist auf die Hälfte verkürzt, also r.
gegeben:
r = 2 cm
h = 6 cm
3d-Skizze der Grundfläche:
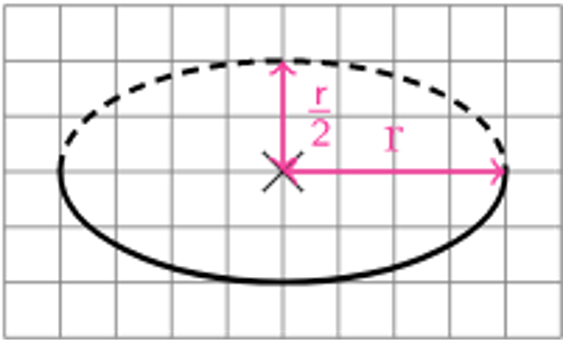
Zeichne vom Mittelpunkt aus die Höhe h ein. Sie endet in der Spitze des Kegels.
Verbinde nun die Spitze mit den Außenpunkten des horizontalen Durchmessers der Elipse.
In dieser Skizze ist die xy-Ebene unverzerrt. Der Radius r, die Höhe h und die Mantellinie s bilden ein rechtwinkliges Dreieck:
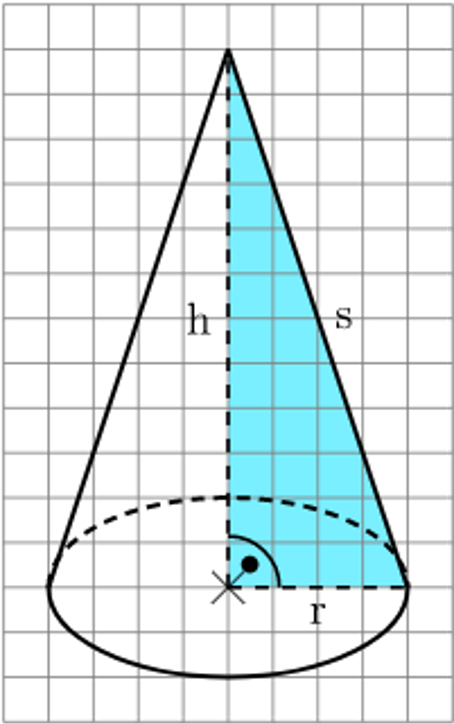
Anmerkungen zur 3d-Skizze:
Die obige Anleitung zur Erstellung einer 3d-Skizze eines Kegels liefert ein schönes Ergebnis, wenn die Höhe h im Verhältnis zum Radius r relativ groß ist. So werden die Beispiele in der Schule in der Regel auch gewählt.
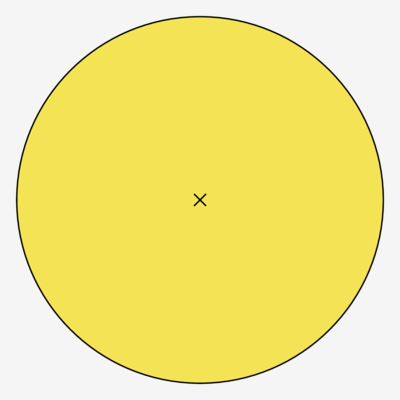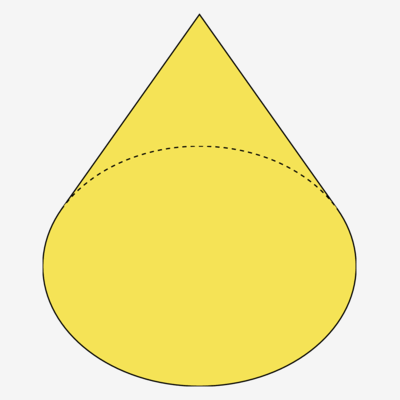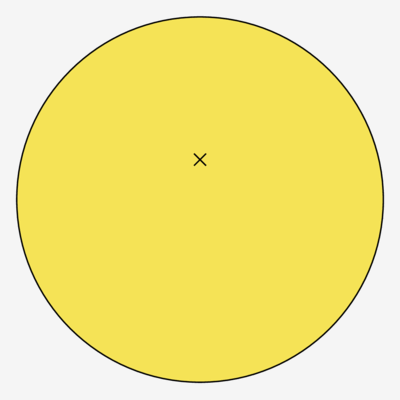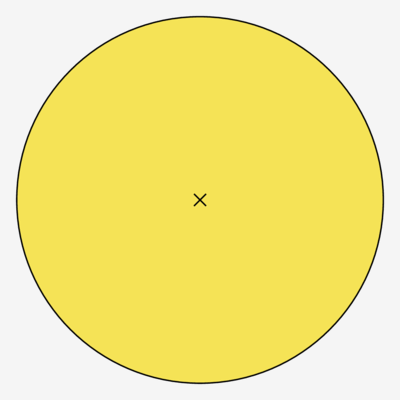
Für kleine Höhen liefert die Kontruktionsanleitung ein unbefriedigendes Ergebnis (egal, wie weit man die Elipse gestrichelt oder durchgezogen zeichnet):
gegeben:
r = 2 cm
h = 2 cm
3d-Skizze:
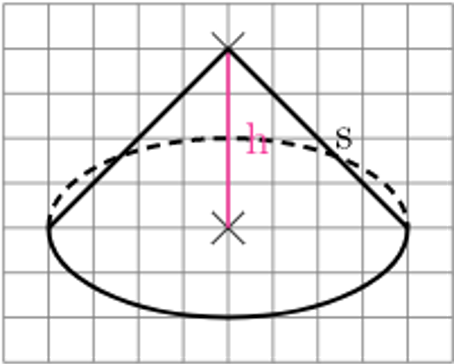
Wenn man einen Kegel auf eine Ebene projiziert, verlaufen die Konturlinien, die die Spitze mit der Elipse verbinden und die Projektion begrenzen, in Wirklichkeit tangential zur Elipse.
Der Unterschied fällt nicht sonderlich auf, wenn die Höhe groß im Verhältnis zum Radius ist. Für kleine Höhen ist hingegen offensichtlich, dass das Bild so aussehen muss:
Die Konturlinie ist nicht identisch zur Mantellinie in der xy-Ebene. Für große Höhen liegen diese beiden Linien jedoch nahe genug beieinander, dass der Fehler nicht auffällt.
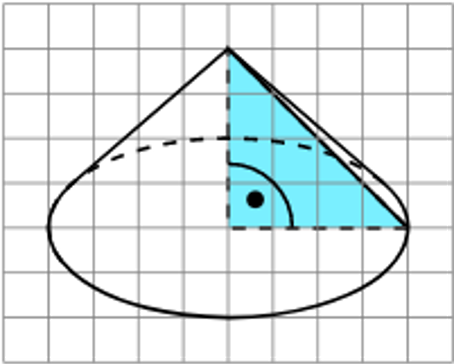
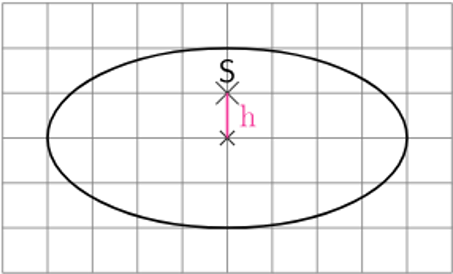
Ist die Höhe im Verhältnis zum Radius noch kleiner, so wird die Elipse vollständig sichtbar und die Spitze fällt in die Elipse. In diesem Fall entfallen die Konturlinien ganz.
gegeben:
r = 2 cm
h = 0,5 cm
Wie auch beim Zylinder liefert ein Schrägbild wie man es für eckige Körper zeichnet, bei dem die Längen in Richtung der z-Achse halbiert und im 45° angetragen werden, kein gutes Ergebnis. Dies gilt auch, wenn die Höhe im Verhältnis zum Radius groß ist.
gegeben:
r = 2 cm
h = 6 cm
Aus der kreisförmigen Grundfläche wird dann eine Elipse, die leicht im Gegenuhrzeigersinn gedreht ist. Entsprechend "verbeult" sieht der resultierende Kegel aus:
Der einzige Vorzug einer solchen Zeichnung ist, dass sie mit dem Schrägbild eckiger Körper konsistent ist und somit ein akzeptables Bild liefert, wenn z.B. ein Kegel in einen Würfel hineingezeichnet wird, siehe hierzu auch den Artikel 3-dim Anschauung und das Schrägbild.
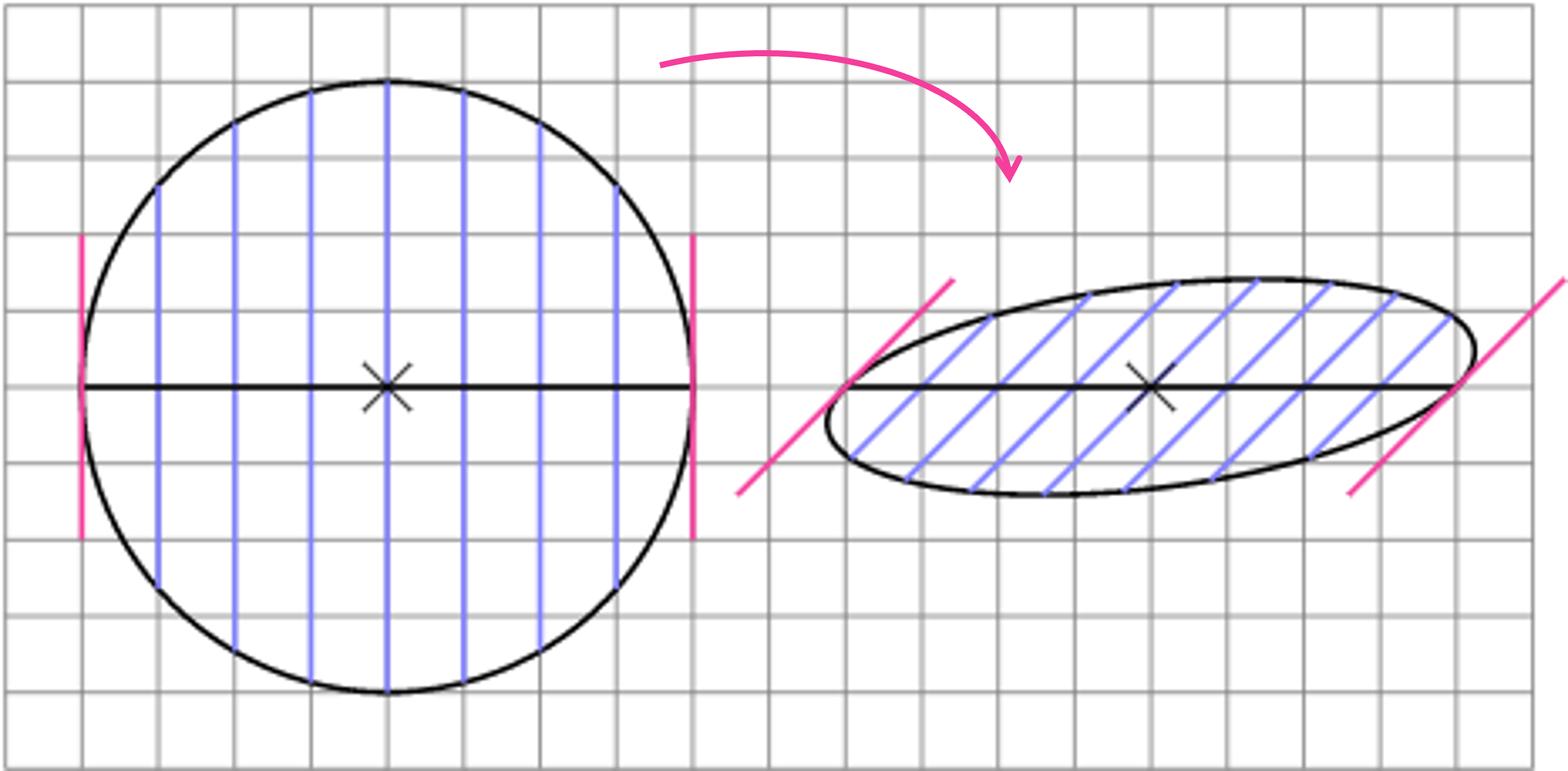
Schrägbild Kegel: