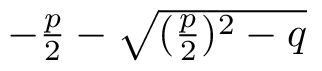Die pq-Formel entdecken

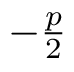
Du hast gelernt, wie du eine quadratische Funktion mit   in Scheitelform bringen kannst.
Wir wollen nun eine   ableiten, damit du diesen Prozess nicht immer wieder durchführen musst.

Gegeben ist die Funktion: . Ergänze quadratisch. Fülle die Lücken.

             

Gib die Scheitelform an:

      . Der Scheitel liegt bei S(  |)

Die Nullstellen liegen also bei:

x₁=             

x₂=