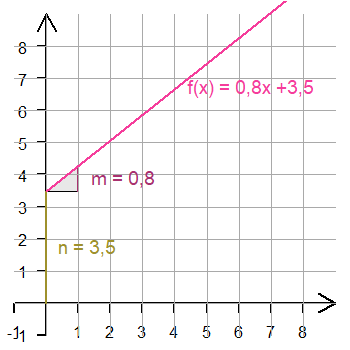Lineare Funktionen
Hier findest du die wesentlichen Merksätze und Regeln zu linearen Funktionen.
Funktionsgleichung
Eine Funktion von einem Definitionsbereich in einen Wertebereich wird durch eine Funktionsgleichung beschrieben.
Mit der Funktionsgleichung kannst du aus einem Wert den zugehörigen Funktionswert berechnen.
Die Funktionsgleichung einer linearen Funktion hat die Form oder .
Dabei sind und feste, gegebene Zahlen.
Definitionsbereich und Wertebereich einer linearen Funktion ist . Du kannst jede Zahl aus in eine lineare Funktion als x-Wert einsetzen oder als y-Wert erhalten.
Beispiele:
oder
, und ist dabei jeweils der Name der Funktion.
Funktionswerte berechnen
Wenn du für x verschiedene Zahlen in die Funktionsgleichung einsetzt, erhältst du die zugehörigen Funktionswerte y.
So kannst du eine Wertetabelle für die Funktion erstellen:
| x | 1 | 2 | 3 |
| y = 4x -5 | -1 | 3 | 7 |
Beispiel:
für
Interaktive Übungen: Funktionswerte berechnen
Punkte auf dem Graphen berechnen
Jede Spalte in der Wertetabelle ist ein Punkt auf dem Graphen der Funktion. Obige Tabelle enthält somit die Punkte P(1|-1), Q(2|3) und R(3|7).
Der Graph einer linearen Funktion ist eine Gerade. Um ihn zu zeichnen, benötigst du nur 2 Punkte.
Zeichne die Punkte aus der Wertetabelle in ein Koordinatensystem ein und verbinde sie mit einer Gerade.

Um zu prüfen, ob ein Punkt auf dem Graphen einer Funktion liegt, setze die x-Koordinate des Punktes in die Funktionsgleichung ein. Wenn der Punkt auf dem Graphen liegt, erhältst du die y-Koordinate des Punktes. Der Punkt S(0,5|-3) liegt auf dem Graphen der Funktion , denn es gilt:
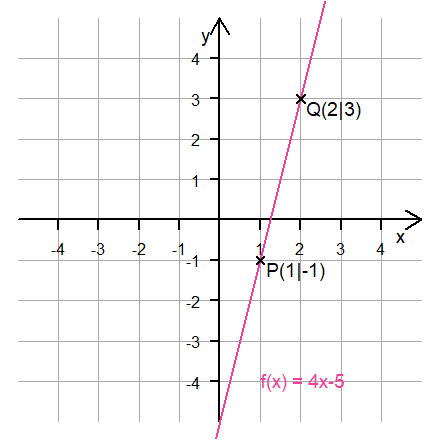
S(0,5|-3) liegt auf dem Graphen. Sie dir die Zeichnung an.
Interaktive Übungen: Punkte auf dem Graphen
Steigung und y-Abschnitt
Bei einer Funktionsgleichung der Form heißt die Steigung und der y-Abschnitt.
Der y-Abschnitt misst wieviel der Funktionsgraph auf der y-Achse nach oben (positiv) oder unten (negativ) verschoben ist.
Die Steigung misst wie steil der Funktionsgraph ansteigt (positiv) oder fällt (negativ).
Die Steigung kannst du mit einem Steigungsdreieck veranschaulichen.
Schau dir die folgenden Beispiele an:

Eine Strasse, die auf 100 m in x-Richtung 8 m in y-Richtung ansteigt, hat eine Steigung von 8/100 = 8%.
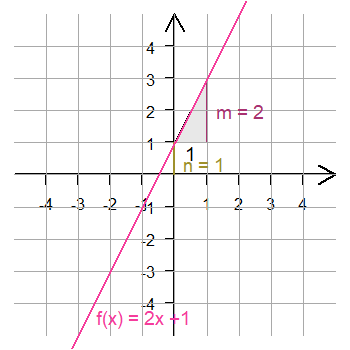
Funktionsgleichung
positiver y-Abschnitt n = 1.
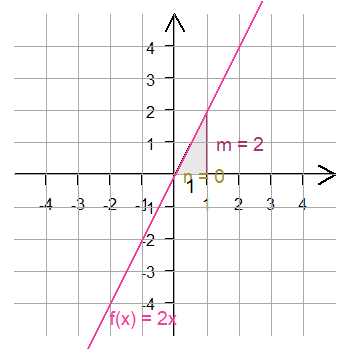
Funktionsgleichung
proportionale Funktion n = 0.
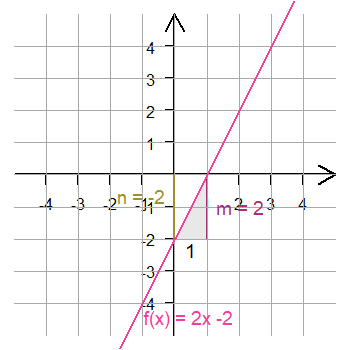
Funktionsgleichung
negativer y-Abschnitt n = -2.
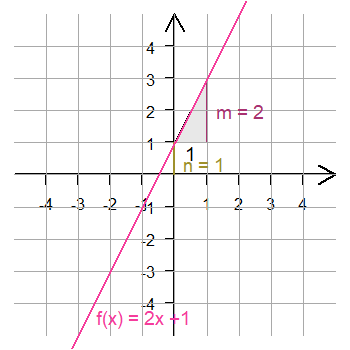
Funktionsgleichung
positive Steigung m = 2.
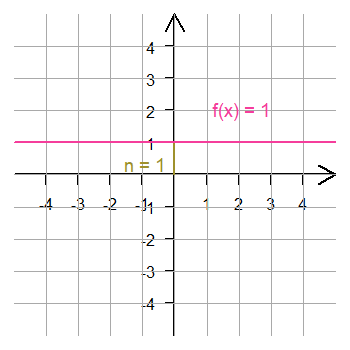
Funktionsgleichung
konstante Funktion m = 0.
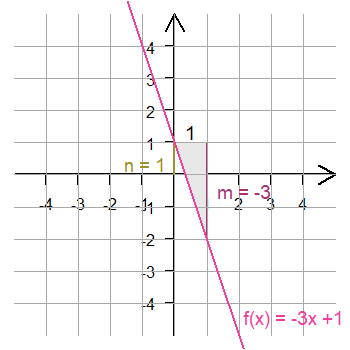
Funktionsgleichung
negative Steigung m = -3
Interaktive Übungen: Graph zeichnen mit Steigung und y-Abschnitt
Argument x aus Funktionswert y berechnen
Bei einer Funktionsgleichung heißt x das Argument und y der Funktionswert.
Wenn du für einen gegebenen x-Wert den Funktionswert y berechnen möchtest, setzt du den x-Wert in die Funktionsgleichung ein und berechnest y.
Wenn du für einen gegebenen Funktionswert y das Argument x berechnen möchtest, setzt du y in die Funktionsgleichung ein und löst die Gleichung dann nach x auf.
Beispiel:
y = -7x + 2. Berechne das Argument zu dem Funktionswert -12.
Setze ein: -12 = -7x + 2
Löse nach x auf: -7x = -14 -> x = 2.
Das Argument ist 2.
oder:
Der Punkt P(?|9) liegt auf dem Graphen der obigen Funktion. Wie lautet die x-Koordinate.
Setze ein: 9 = -7x + 2
Löse nach x auf: -7x = 7 -> x = -1.
Es ist der Punkt P(-1|9)
Interaktive Übungen: x-Wert berechnen
Nullstelle berechnen
Die Nullstelle ist die x-Koordinate, wo der Graph die x-Achse schneidet. Das heißt, wir suchen den Punkt P auf dem Graphen mit y-Koordinate 0.
Setze also y = 0 in die Funktionsgleichung ein und löse nach x auf. Die berechnete x-Koordinate ist die Lösung. Die Nullstelle liegt also bei
Du kannst die Nullstelle auch aus dem Graphen ablesen.
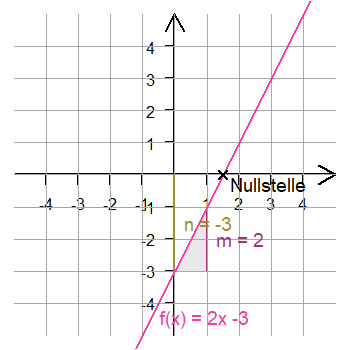
Die Nullstelle ist x = 1,5.
Interaktive Übungen: Nullstelle berechnen
Funktionsgleichung aufstellen
Manchmal kannst du Werte, die von einem anderen Wert abhängen als Funktionsgleichung darstellen.
Beispiel
Die Kosten einer Taxifahrt pro km sind 3,50 € zuzüglich 0,80 € pro km.
Erklärung:
Berechnet werden Kosten pro gefahrene km -> y = f(x)
Ein Teil der Kosten ist ein Faktor m mal die gefahrenden km (x). -> mx
Ein Teil der Kosten ist konstant -> n
Die Funktionsgleichung ist also
Der Definitionsbereich der Funktion sind hier nur positive Zahlen , denn man kann keine negativen Kilometer fahren.